在行测数量关系的题目中,我们经常会遇到求最值的问题,和定求最值是其中的一种题型。今天跟大家研究一下这类问题怎么做,以及如何运用“小系数同方向”的口诀来解题。
例题
有100个人参加某企业的招聘考试,每人需答对5道题,统计后1-5题答对的人数分别为74人,90人,88人,77人和81人,按照规定答了3题或3道以上的人员算通过考试,请问至少有多少人能通过考试?
a.40 b.65 c.70 d.74
【答案】c。解析:1-5题做对的总数量为74 90 88 77 81=410题,设有x人通过,有y人未通过,根据题意有(3、4、5)x (0、1、2)y=410,由“小系数,同方向”知,优先确定y的系数,要想通过的人尽量少,则未通过的人应尽量多,y应取最大系数2,则5x 2y=4101,x y=100,联立两式解得x=70,即至少有70人能通过。
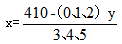
【思维点拨】题目参加考试的人共100人,1-5题做对题目数共74 90 88 77 81=410题,我们可以据此列方程。题目求“请问至少有多少人能通过考试”,我们设有x人通过,有y人未通过。根据等量关系式列得x y=100,(3、4、5)x (0、1、2)y=410。这个方程组我们可以看到第二个式子x和y的系数不确定,无法直接求解。我们要求的是x的最小值,将原始转化为。分析可知:x要小,则y的系数应尽可能大,取2;分母要尽可能大,取5为x的系数。则方程为x y=100,5x 2y=410。联立两式解得x=70,即至少有70人能通过,选 c项。
当我们遇到:所求量包含了一定范围的和定最值问题时,可以借助“小系数同方向”的口诀来求解。具体运用为我们列出方程后,系数不确定时,找到小系数对应的未知数,判断它的取值情况:小系数对应的未知数需取最大值时,所有系数同时取大的;小系数对应的未知数需取最小值时,所有系数同时取小的。
接下来就让我们运用口诀来解一下这个题。根据等量关系式列得x y=100,(3、4、5)x (0、1、2)y=410。这个方程组我们可以看到第二个式子x和y的系数不确定,无法直接求解。由“小系数,同方向”知,y为小系数对应的未知数,判断它的取值情况:因为总人数100为定值,要求通过的人的最小值,则未通过的人应尽可能大,即y需取最大值,所有系数同时取大的5x 2y=410。联立两式解得x=70,即至少有70人能通过,选 c项。
我们不难发现运用口诀解决这类特殊的和定最值问题会更容易一些,且熟练运用后也不容易出错,希望大家能够熟练掌握。







